1980年终于解决的数学谜语-可用于改进电话和计算机

时间：2022-02-16 12:58:06来源：

两位计算机科学家，UCPH的助理教授Jacob Holm和DTU的Eva Rotenberg副教授，在提交了一篇研究文章（该文章最终解决了数学之谜）的先驱之后，几乎在2019年夏天放弃了他们的解决方案。

研究人员认为，距离解决1980年代的数学难题还有5年的时间。实际上，在不知情的情况下，他们已经几乎破解了这个问题。

哥本哈根大学和丹麦技术大学（DTU）的研究人员认为，距离解决1980年代的数学难题还有5年的时间。实际上，在不知不觉中，他们几乎破解了这个问题，并在一篇研究文章中放弃了很多解决方案。该解决方案可用于改进明天的电话和计算机。

名副其实的脑筋急转弯。这样便可以在图论学科中安全地描述这一数学问题。哥本哈根大学计算机科学系和DTU的两位数学家现在解决了自1980年代以来世界上最快，最聪明的难题。

“我们几乎放弃了获得最后一块并解决难题。我们认为我们取得了次要的结果，这很有趣，但绝不能解决问题。我们猜测，要想解决这个难题，最多还需要五年的时间。” UCPH计算机科学系算法部门BARC的成员Jacob Holm解释说。

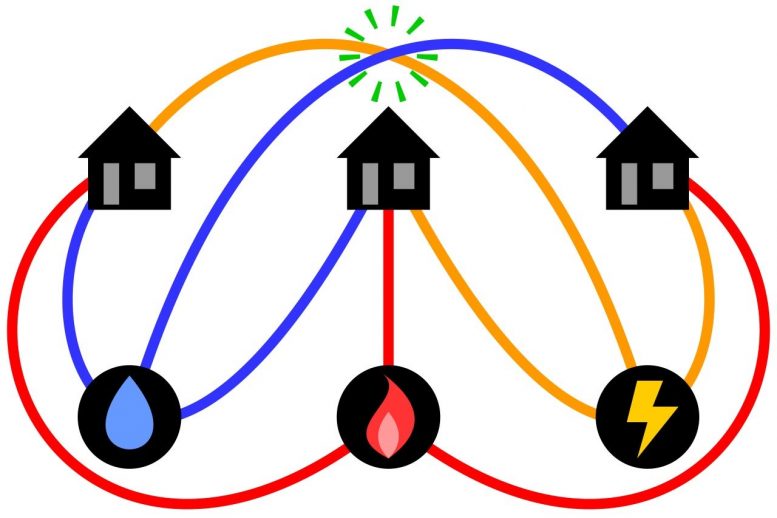
1913年，现在已解决的数学难题的前身在“斯特兰德杂志”（The Strand Magazine）上发表为“三个公用事业问题”。这使该杂志的读者挠头思索。问题是，三栋小屋中的每栋都必须有水，气和电，而房屋与水，电和气之间的“界线”可能无法相互交叉，这是不可能的。

简而言之，难题是关于如何在图形中连接多个点而又不让连接它们的线交叉的问题。以及如何通过数学计算（一种算法）来更改广泛的“图形网络”，以确保没有线相交而无需重新开始。除其他事项外，这些属性可用于构建巨大的道路网络或计算机内部的微小内部，其中电路板上的电路可能不会交叉。

自1998年以来，雅各布·霍尔姆（Jacob Holm）就对数学难题产生了兴趣，但答案只有在两名研究人员通读他们已经提交的研究文章时才透露出来。同时，研究人员听说了一种新的数学技术，他们意识到可以将其应用于该问题。

“在阅读我们的研究文章时，我们突然意识到解决方案摆在我们眼前。DTU的副教授Eva Rotenberg说，我们的下一个反应是“哦，不，我们已经把自己打倒了，放弃了解决方案。”

这是两位研究人员忙于撰写研究论文并绑扎松散的末端以解决Holm自1998年以来就断断续续工作的难题的时候。

“我们连续五到六周研究了这篇文章。而且，最终它填满了80多页，”伊娃·罗滕伯格（Eva Rotenberg）说。

幸运的是，没有人击败他们，并且两位研究人员能够在原定于芝加哥举行的主要理论计算机科学会议上展示他们的结果，但最终还是以虚拟形式举行。

那么，该数学难题的解决方案可以用于什么呢？两位研究员不确定，但他们有一些建议。

“我们的研究是基础研究，因此我们很少知道它最终将被用作什么。甚至从一开始，我们就发现难以想象的应用程序。” Jacob Holm补充说：

“所有电子产品中都存在微芯片和电路板的设计，这可能是我们最终使用该技术的领域。在电路板上绘制电线时，它们不得相交。否则会发生短路。同样的情况也适用于微芯片，其中包含数百万个晶体管，并且必须具有一个图形图。”

GRAPH是一种非常简单的构造，用于对事物进行建模，这些事物可以描述为对象及其之间的连接。图论既是数学领域，也是计算机科学中的重要工具。

在这种情况下，可以通过由与多个线（边缘）相关联的多个点（节点，顶点）组成的图来说明图。每个边缘都显示为一条线（或弯曲的片段），其节点为两个端点。

动态图中有两种更新：可以删除边线，也可以插入新边线。这两个操作必须由用户执行，而算法则始终保持跟踪网络的图形。这是研究人员找到配方的算法。

参考：Jacob Holm和Eva Rotenberg的“多对数时间全动态平面性测试”，2019年12月10日，计算机科学>数据结构和算法。
1911.03449