【每日一题】化学实验基本知识点（二）

《大学物理-PPT课件：06机械能守恒.ppt》会员共享，可在线阅读。更多相关《大学物理-PPT课件：06机械能守恒.ppt（26页珍藏版）》，请下载图书馆搜索。

1、一、功一、功在描述空间力的累积作用时描述力的累积作用1、恒力功：，恒力功：ab 3、合力做功，合力做功：2、变力做功，变力做功，变力做功，变力做功力，力的功，力的功，合力的功，合力的功，合力的功，合力的功，合力的功，合力的功，合力的功。功率：瞬时功率：瞬时功率：二、粒子动能定理二、 粒子动能定理 动能是动能是状态量；工作是；工作是过程量。三、粒子系统的动能定理三、粒子系统增量的动能定理。增量。2一、一、共力功2.32.3 泛函原理与机械能守恒定律 泛函原理与机械能守恒定律1. 万有引力重力功 重力功的特点： 重力功的特点：只配只配

2、运动物体的运动物体的起止位置与起止位置有关，与运动物体经过运动物体的路径无关。当物体沿任意闭合路径绕行时，当物体沿任意闭合路径绕道时，重力做的功为零，重力做的功为零。32.万有引力做功的特性万有引力做功的特点：万有引力做功与路径无关，只有功与路径无关，只有起点和终点位置. 它与开始和结束位置有关。43. 弹力做功 弹力做功 弹力做功只由物体的起点和终点位置决定，与路径无关。如果物体沿任意闭合路径绕圆，则如果物体沿任意闭合路径绕圆，则 5二、保守力和非保守力二、保守力和非保守力独立工作路径的，只与路径有关。起止位置与作品有关，路径与它无关，仅 保守和非保守力量确实独立于路径工作，只与路径有关。起止位置与作品有关，路径与它无关，仅 保守和非保守力量确实独立于路径工作，只与路径有关。起止位置与作品有关，路径与它无关，仅

非守恒力非守恒力-摩擦力做功 摩擦力的功等于与起止位置和起止位置有关的两个函数之差的差值。势能函数增量 保守力所做的功等于该保守力所做的功 负防御力阶段等于该保守力对应的势能增量

4、对应势能增量的负值 8 指参考位置 位置势能 势能零点 零点（2） 选择时） 选择 2 位置势能即为位置势能为 0 A1-2= EP1 系统某位置的势能 系统某位置的势能 = 系统从该位置变为势能 系统从该位置变为势能为 0 所做的功位置 9 的守恒力 弹性势能 弹性势能 引力势能 引力势能 引力势能 引力势能 万能引力势能 00r 2.几种保守力对应的势能 几种保守力对应的势能为0 地势能为地势能为0 地上方为正势能 地上方为正无穷大势能，无限远距离 势能为0，任意点为负 任意点为负平衡位置 势能为平衡位置 势能为0，任意点为正 任意点为正 103.几点说明概念的介绍的保守力场 (this) 势能是地面以上为正势能 地面以上为正无穷势能，无穷远距离势能为0，任一点为负 任一点为负平衡位置 势能为平衡位置 势能为0，任一点为正任意一点都是正的 103.几点说明 保守力场（this）势能概念的引入是地面以上为正势能 地面以上为正无穷势能，无穷远距离势能为0，任一点为负 任一点为负平衡位置 势能为平衡位置 势能为0，任一点为正任意一点都是正的 103.几点说明 保守力场（this）势能概念的引入是几点解释 保守力场（this）势能概念的引入是几点解释 保守力场（this）势能概念的引入是

5、基于物体处于保守力场中（2）势能也是一个状态量，与势能和动能不同）势能也是一个状态量，势能不同于动能。区别 动能是粒子速度的函数 动能是粒子速度的函数 势能是粒子位置坐标的函数 势能是粒子位置坐标的函数（3）势能有） 势能有相对性，它的值和势能零，它的值与势能零点的选择有关（4）势能属于系统。本质上，势能是一种相互作用）势能属于系统。本质上，势能是一种相互作用能。对于单个物体，没有使用势能，对于单个物体，没有势能。势能差具有绝对绝对性，与势能零点有关机械,功和机械能，与势能零点的选择无关。例如，引力势能是由物体和地球组成的系统。例如，引力势能是 这与势能零点有关，与势能零点的选择无关。例如，引力势能是由物体和地球组成的系统。例如，引力势能是 这与势能零点有关，与势能零点的选择无关。例如，引力势能是由物体和地球组成的系统。例如，引力势能是

6、身体和地球所做的功（5）非保守力所做的功会随着所走的路径而变化，即）非保守力所做的功会随着所走的路径而变化所走的路径不同，即其值是不确定的，因此无法引入与之相关的势能。它的值是不确定的，因此无法引入与之相关的势能。11 系统强制系统强制外力外力内力保守内力保守内力非保守内力非保守内力四、作用原理四、

7、没有变化。系统中粒子之间的动能和势能可以相互交换和转化。粒子之间的动能和势能可以相互交换和转化。（2）机械能守恒定律的条件）机械能守恒定律的条件是没有外力，没有外力，非保守内力，外力，非保守内力，但不工作，外力​​，非保守内力，但不工作。系统中的非保守内力不等于系统中的非保守内力。当非保守内力不为零时，机械能不守恒。机械能守恒定律只适用于惯性系统。13 用函数原理和机械能守恒定律解题时注意：用函数原理和机械能守恒定律解题注意：1.系统适用范围应该指定，以便区分范围，以便区分内力和外力和外力，因为，对于内力，需要区分

8、对于力，也需要区分保守内力和非保守内力。保守内力和非保守内力，判断守恒，判断守恒条件是否成立：对于保守内力，可以引入相关势能。条件是否成立：对于保守内力，可以引入相关势能。2.在列出方程之前，必须将质点系统中的物理量统一到同一个惯性系统中，这样才能正确计算出每个力的功和每个质点的功。为了正确计算每个力的功和每个粒子的动能3. 表示各个相关势能的零势能位置和各个相关势能的零势能位置，然后理清系统，进而理清系统的起点和终点在机械能状态的末端。机械能。14 在自然界中，任何系统都有能量，并且有不同种类的能量

9、形式，从一种形式，可以从一种形式转换成另一种形式，从一个对象传递到另一个对象（或系统），在对象到另一个对象（或系统）的变换和传递中，在在转化和传递的过程中，能量不会消失，也不会被创造出来。在这个过程中，能量不会消失，也不会被创造出来。这个结论被称为能量守恒定律。能量守恒定律称为能量守恒定律，如果系统有一个非保守的内力，而这个非保守的内力）做负功，系统的机械能就会减少。（如摩擦）作负功，系统的机械能就会降低。但大量事实证明，在机械能减少的同时，必然还有其他形式的能量增加。能量增加的形式。例如，通过克服摩擦做功

10、当机械能减少时，必然产生热量。例如，当机械能由于克服摩擦力而减少时，必须产生热量。热热。然而，它是一个。然而，它是另一种超越机械能的能量形式。另一种超越机械能的能量形式。实验证明，能量可以相互转化，但总量保持不变。实验证明，能量可以相互转化，但总量保持不变。六、能量守恒定律六、能量守恒定律15 两块木块的质量分别是m1和m2，两块木块的质量分别是m1和m2，和 m2 = 3 m1 , 两用一用，光用一用 光弹簧连接好后机械,功和机械能，靠在光滑平整的水平面上，再靠在光滑平整的水平面上，如图所示。现在用外力将两块木块用外力压在一起，使弹簧被压缩块压住 几乎使弹簧被压缩x0

11、，然后去掉外力再去掉外力，求后续过程中的守恒量从原长度求后续过程中的守恒量k 最大伸长率：最大伸长率：思考题思考题1：从放手到放手原长：原长：只有弹力（保守内力）只有弹力（保守内力）做功，做功机械能守恒，机械能守恒弹簧的势能转化为动能，此时弹簧的势能转化为动能，这在木块即将移动的时候。所以只有积木即将移动。所以只有2个动能。动能。1 木块移动后，系统仍无外力，动量守恒。木块移动后，系统仍无外力，动量守恒，机械能守恒，机械能守恒。一端和一端固定在地面上，另一端连接质量为m的物体，质量为m，质量为m的泥球在泥球的正上方就在上面。

12、 在 h 的高度自由落体到 M，求 m 的最大位移和与 M 粘在一起的运动？运动的最大位移？从 m 落下 静止仍落在 M 上： on： 从 mM 移动 最大压缩： 最大压缩： 碰撞 碰撞（完全无弹性完全无弹性） 过程： 过程： 加上 M 与弹簧初始平衡条件和弹簧初始平衡条件 问题问题 问题 2：机械能守恒 动量守恒 动量守恒 机械能守恒 机械能守恒 选择图中的位置是重力势能的零点。弹簧的原始长度为零势能。选择图中的位置是引力势能的零点。17 示例 示例 1. 质量为 m 的珠子系在电线的一端，电线的另一端系在墙上，珠子系在电线的一端，电线的另一端系在到墙上的一个钉子，金属丝的长度是 钉子上，金属丝的长度是 l。先拉珠子保留线材

13、保持水平不动，然后先拉珠子让线保持水平不动，然后松开手让珠子落下，再松开手让珠子落下。求线下摆时珠子的速度，求线摆角处珠子的速度 解法：以珠子和大地为系统 以珠子和大地为系统，取挂点线的高度和线的悬挂点O的高度作为重力势能零点的高度，重力势能零点，机械能守恒，机械能守恒。解释： 解释：弹簧的顽固系数 光滑平面上的弹簧系统，弹簧的顽固系数 k = 24 N/mm，物体的质量，物体的质量 m = 4 kg kg。现在使用恒力。现在使用恒力 P=10 牛顿 弹簧的顽固系数 光滑平面上的弹簧系统，弹簧的顽固系数 k = 24 N/mm，物体的质量，物体的质量 m = 4 kg kg。现在使用恒力。现在使用恒力 P=10 牛顿

14、牛顿将物体拉离平衡状态，将物体从静止状态拉离平衡位置（弹簧的原始长度），如图所示。寻找：将其拉离静止，如图所示。求：(1)物体在力P的作用下运动。作用下，物体运动S1=0.5米处的速度；所在位置的速度；(2)@ >Pull to pull 当在0.5米处去掉恒力时，物体可以向前移动多远，物体可以向前移动多远?取弹簧中物体和物体的原始长度在弹簧的原始长度中弹性势能的零点是弹性势能的零点。 19 物体和弹簧被视为整体物体，弹簧被视为整体，

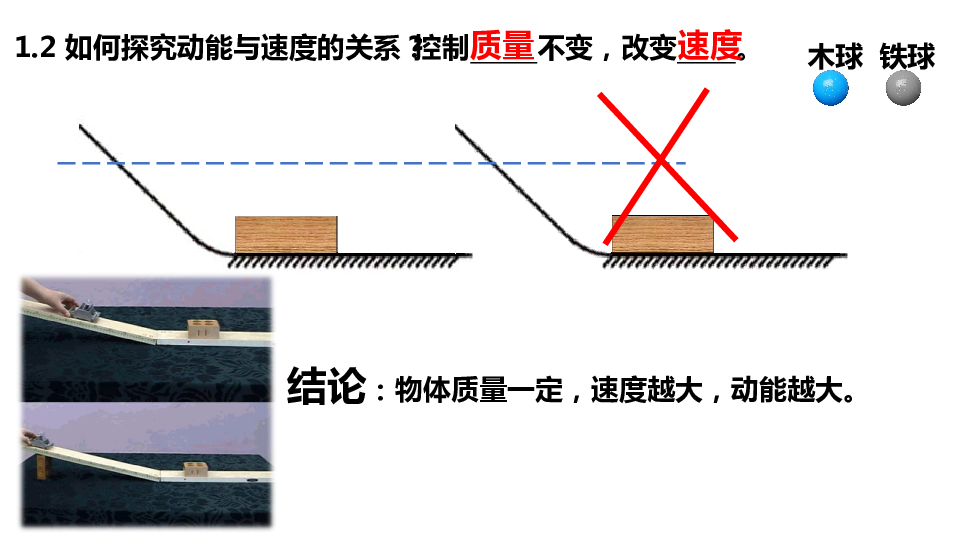
15、从A点出发的小球在外力作用下开始做匀加速直线运动，从A点出发，到达B点时，外力取消，球没有摩擦。当外力取消时，小球无摩擦地冲进一个垂直半径为R的半圆，半圆刚好到达最高点，到达最高点C，然后刚好到达最高点C、当它落到原来的起点，刚好落到原来的起点A时，如图所示，试着找出小球在哪里。如图，小球在AB段运动的加速度是多​​少？段运动的加速度是多​​少？解决方案： 解决方案：因为小球可以在C点做圆周运动，所以这个点只能做圆周运动。因此，以小球与地为系统，以小球与地为系统，BC段的机械能守恒。节段的机械能是守恒的。选择大地作为势能零点，大地作为势能零点。21AB的长度是

16、球的长度是球在AB段的匀加速度和匀加速度直线运动。球从 C 到 A。这是一个平抛运动。它移动并以 vc 作为初始速度。小是初速度，球从C到A所需要的时间是t 22 一个质量为m=2kg的块在一个四分之一圆弧的滑道上运动 从A点移动到B点四分之一灭弧室，给定点，给定 vA=0，vB=6m/s，R=4m，g=10m/s2，求 Find AB，Af=? 解法： 解法： 方法一：使用功的一般定义 使用功的一般定义 例4:23 方法 方法二：使用粒子动能定理 使用粒子动能定理（质量）（块） 方法三：使用泛函原理 使用泛函原理（以块体和地球为研究对象）（以块体和地球为研究对象） 24一、保守力做功的特征一、特征守恒力所做的功 1. 当物体沿任何闭合路径绕着闭合路径绕行时，守恒力所做的功在一圈内为零。努力为零。工作与路径 没有工作与路径无关，只有开始和结束，只有开始和结束的位置。位置相关。总结25二、势能二、势能弹性势能弹性势能引力势能引力势能引力势能引力势能三、