研究人员开发了一种新的Quantum误差纠正码

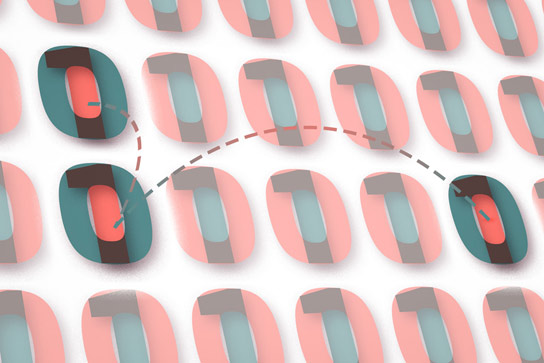
来自麻省理工学院，谷歌，悉尼大学和康奈尔大学的研究人员呈现了一种新的Quantum误差校正代码，需要一次测量几个量子位，以确保计算的一个阶段和下一个阶段之间的一致性。

量子计算机主要是理论设备，可以比传统计算机符合速度的速度执行一些计算。对于量子计算机的大多数设计至关重要是量子误差校正，这有助于保持量子计算取决于哪些易碎量子状态。

理想的量子纠错码将纠正量子数据中的任何错误，并且需要一次测量几个量子位或QUBITS。但到目前为止，可以使用有限的测量执行的代码可以纠正有限数量的错误 - 一个大致等于Qubits总数的平方根。因此，它们可以在64态量子计算机中纠正八个错误，例如，但不是10。

在一篇论文中，他们在6月份计算机械管理机构专题讨论会上，麻省理工学院，谷歌，悉尼大学和康奈尔大学的研究人员展示了一个可以纠正痛苦的错误 - 几乎 - 一个指定的分数计算机的Qubits，不仅仅是他们的号码的平方根。并且对于合理大小的量子计算机，该分数可以是任意大的 - 尽管它的越大，计算机需要的额度就越多。

“许多不同的建议，所有这些建议似乎都陷入了这种平方根，”麻省理工学院的物理学助理教授Aram Harrow说，他领导了研究。“所以超越这是我们对这项工作感到兴奋的原因之一。”

与传统计算机中的一点一样，一个量子位可以表示1或0，但它也可以居住称为“量子叠加”的状态，其中它同时表示1和0。这是量子计算机潜在优势的原因：在某种意义上，叠加中的一串Qubits可以并行执行大量计算。

但是，在Qubits上执行测量，叠加折叠，并且Qubits对明确的值。量子算法设计的关键是操纵QUBITS的量子状态，使得当叠加折叠时，结果是（具有高概率）解决问题。

宝贝，浴盆

但需要保护叠加的需要使难以纠正困难。“人们认为在90年代不可能进行错误纠正，”哈罗解释说。“这似乎是p出来你必须测量的错误，测量会破坏你量子信息。”

第一个量子纠错码于1994年由Peter Shor发明，现在是MIT应用数学教授的MIT教授，距离哈罗的大厅里有一个办公室。 Shor还负责将量子计算放在地图上的理论结果，这是一种算法，该算法将量子计算机能够比传统计算机符合速度的速度较大。事实上，他的错误校正码是对对实施他的要素算法的可行性的怀疑态度。

Shor的Insight是可以测量Qubits之间的关系，而不会测量Qubits本身存储的值。例如，可以将一个简单的错误校正代码实例化为三个物理Qubits的数据。可以确定第一和第二Qubbit是否具有相同的值，以及第二个和第三QUB是否具有相同的值，而无需确定该值是值。如果其中一个Qubits拒绝不同意其他两个，则可以重置为其值。

在量子误差校正中，哈罗解释，“这些测量总是具有”形式“与B？'不同意除了它可能是，而不是a和b，一个完整的东西块。这些类型的测量，在真实的系统中，可能很难做到。这就是为什么它真正需要减少你必须立即测量的Qubits数量。“

时间体现了

量子计算是量子位状态的连续。比特在某种状态;然后他们被修改，所以他们承担另一个国家;然后他们再次修改;等等。最终状态代表计算结果。

在他们的论文中，哈罗和他的同事分配了每个公司的计算额外的Qubits银行;这就像将计算的时间尺寸转化为空间尺寸。假设在时间5时的Qubit 8的状态对时刻6的Qubit 8和Qubit 11的状态具有影响。研究人员的协议对所有三个Qubits进行了一个协议测量，修改了与另外两个相对对齐的任何Qubit的状态。

由于测量没有揭示任何Qubits的状态，因此对未对准的Qubit的修改实际上可以引入未以前存在的错误。但这是通过设计：该协议的目的是确保错误以合法的方式通过贵族来传播。这样，在Qubits的最终状态下进行的测量得到保证，以揭示Qubits之间的关系，而不会揭示其值。如果检测到错误，则协议可以将其追溯到其原点并更正。

可能有可能在没有实际复制Qubits银行的情况下实现研究人员的计划。但是，Harrow说，可能需要在硬件中进行一些冗余来使方案有效。仍有多少冗余待地看出：当然，如果计算每个状态所需的Qubits银行，那么计算机可能会变得如此复杂，以抵消良好纠错的优势。

但是，哈罗说：“几乎所有的稀疏方案都开始出现并不是很多逻辑夸张，然后人们会得到更多的方式。通常，增加逻辑Qubits的数量比增加距离更容易 - 您可以纠正的错误数。所以我们希望这将是我们的案例。“

悉尼大学的物理教授Stephen Bartlett研究量子计算，并没有找到哈罗和他的同事计划特别令人生畏所需的额外贵族。

“看起来很多，”巴特利特说，“但与现有结构相比，这是一个大幅减少。所以这种建设的一个亮点是他们实际上得到了很多。“

“人们拥有这些代码的例子，这是非常糟糕的，受到平方根'n的限制，”Bartlett补充说。“但人们试图把界限放在可能的可能性，而这些界限也表明你可以做得更好。但我们没有得到这里的建设性的例子。这就是让人兴奋的东西。我们知道我们现在可以到达那里，现在这是一个更加实用的问题。“

研究报告的PDF副本：来自量子电路的稀疏量子码

图像：荷西-路易斯·奥利瓦雷斯/麻省理工学院